Introduction
Medical diagnosis is a multifaceted endeavour that relies on a comprehensive assessment of various factors, including symptoms, tests, and medical history. Conditional probability, which calculates the likelihood of an event occurring given another event, plays a pivotal role in evaluating the effectiveness of medical diagnoses. In the context of healthcare, this involves estimating the probability of a patient having a disease, given that they have tested positive for it.
Understanding Accuracy
One of the most commonly used metrics in medical diagnosis is accuracy. It gauges the overall proportion of accurate diagnoses, derived from correctly identifying patients with or without a specific ailment. Accuracy can be mathematically expressed as a combination of sensitivity and specificity, both of which are vital metrics.
\(Accuracy = Sensitivity \times Prevalence + Specificity \times (1 - Prevalence)\)
Sensitivity and Specificity
Sensitivity measures the ability of a diagnostic method or model to correctly identify patients who have the disease, while specificity measures its ability to accurately identify those without the disease. These metrics can also be understood in terms of conditional probabilities, simplifying them to the probability of a positive or negative test result given a patient’s disease status.
\(Sensitivity = \dfrac{\,number\,of\,positive\,and\,disease}{\,number\,of\,disease}\)
\(Specificity = \dfrac{\,number\,of\,negative\,and\,normal}{\,number\,of\,normal}\)
In terms of conditional probabilities:
\(Sensitivity = P(positive|disease)\) \(Specificity = P(negative|normal)\)
Positive Predictive Value and Negative Predictive Value
To assess the likelihood of a patient having or not having the disease based on their test results, we employ positive predictive value (PPV) and negative predictive value (NPV). These metrics provide insight into the probabilities of disease presence or absence given a positive or negative test result, respectively. This is more useful and practical than just sensitivity and specificity
\(PPV = \dfrac{\,number\,of\,positive\,and\,disease}{\,number\,of\,positive}\)
\(NPV = \dfrac{\,number\,of\,negative\,and\,normal}{\,number\,of\,negative}\)
Leveraging Bayes’ Rule:
To calculate PPV and NPV, Bayes’ rule, a formula relating conditional probabilities, is employed. This rule offers a nuanced perspective by taking into account sensitivity, specificity, and prevalence—the proportion of patients with the disease in the population.
Using conditional probabilities, we write:
\(PPV = P(disease|positive)\)
\(NPV = P(normal|negative)\)
Confusion Matrix
A confusion matrix serves as a valuable tool to visualize the performance of a diagnostic method or model. It displays true positives, true negatives, false positives, and false negatives for different thresholds or cut-off points, which can be adjusted to modify the diagnostic performance metrics.
A confusion matrix can be represented as:
| Positive | Negative | |
|---|---|---|
| Disease | TP | FN |
| Normal | FP | TN |
where: TP = True Positives (number of)
FP = False Positives
FN = False Negatives
TN = True Negatives
Precision and Recall
Precision measures the proportion of correctly identified positive test results, while recall assesses the proportion of patients with the disease that are accurately identified. These metrics are also synonymous with positive predictive value (PPV) and sensitivity, respectively.
\(Precision = \dfrac{TP}{TP+FP}\)
\(Recall = \dfrac{TP}{TP+FN}\)
Precision and recall are also known as positive predictive value (PPV) and sensitivity, respectively. Therefore, they are equivalent to:
\(Precision = PPR\)
\(Recall = Sensitivity\)
F1-Score
The F1-score combines precision and recall into a single metric, which is the harmonic mean of both values. This metric is also known as the Dice coefficient score, reflecting the similarity between two sets.
\(F1\,Score = 2 \times \dfrac{PR}{P+R}\)
Evaluating Diagnostic Methods with ROC Curves
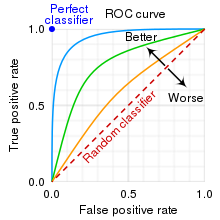
To compare different diagnostic methods or models, the receiver operating characteristic (ROC) curve is a valuable tool. It illustrates the trade-off between sensitivity and specificity at varying thresholds. A high-performing diagnostic method or model should yield a ROC curve closely resembling the top-left corner of the plot, with the area under the ROC curve (AUC) indicating its overall performance.
Conclusion
The multifaceted landscape of medical diagnosis evaluation encompasses a spectrum of metrics and tools. Understanding these metrics and their mathematical underpinnings is crucial for accurately assessing the performance of diagnostic methods and models in healthcare.